Haversine Formulas (Or ACOS/COS/SINor SQT) Not functioning with Sensor Location

[cresto.pgaxq2]

Anyone having issues with syncing live LAT and LONG to the haversine formula. This started not too long ago. I went back through and tried some elements to resolve variable operations.

But not getting correct math. I have ran it against Excel Formula for measuring distance. I have it converting into yards. It worked not too long ago.

The app keeps jumping between two calculations. Even though I move around right now it either goes to 97 yards or 138 yrds.

Not sure if it is functionality with coded blocks.

0.07922

[cresto.pgaxq2]

or it bounces into 0.0560168856

Its not even close.

Excel is spot on. Using this formula

=ACOS(COS(RADIANS(90-Lat1)) *COS(RADIANS(90-Lat2)) +SIN(RADIANS(90-Lat1)) *SIN(RADIANS(90-Lat2)) *COS(RADIANS(Long1-Long2))) * 3958.76

I then multiply that number by 1760( yards in a mile)

Spot on.

App is not

[tatiang]

The first rule of getting help on the forums is to show your work. But we can’t see your blocks and we don’t have a link to your project. So there’s no way we can help you yet. See this: How to ask Great Questions v2.0.

[cresto.pgaxq2]

Here is what Im comparing to in excel. the 108 is correct. 139 is not. The precalculation isnt correct. I even put in (PI) vs. the pie symbol in thunkable. Even adding the symbol back in it doesnt work.

[cresto.pgaxq2]

I also adjusted the multiplier (3959.87) just to see if anything changes

Not sure why they are different. I have messed around with a ton.

[cresto.pgaxq2]

I changed the multiplier to 3050. Numbers match. But, that means one of the math flows is not correct

[cresto.pgaxq2]

Just sent some details to you

Thanks!!

[cresto.pgaxq2]

I have also tried converting all variables into text blocks. So it is absolute. Still the same math error. This was working not too long ago. Very frustrating. Not sure which update caused the issues.

[tatiang]

@cresto.pgaxq2

Just sent some details to you

In a private message? I don’t see one from you.

[cresto.pgaxq2]

Just in the messenger

I’m looking back at old app inventor logs

Would love to process this through excel 365 to do the math as data inputs.

But want the calculations to go fast through the app.

I’m not sure why it’s not computing.

[tatiang]

@cresto.pgaxq2

Just in the messenger

What do you mean by that? The only way I’m aware that you can contact another user is through private messages or by notifying them using the @ symbol like @cresto.pgaxq2.

I sent you a project by PM that works for me. But you mentioned the calculations are off so I’m not sure what else to recommend.

[cresto.pgaxq2]

Do you get the same output in your app from the last screenshot I sent from the third party site.

If you use the lat and longs I saved

Please let me know

Or if you have any insight into the calc error

[tatiang]

You have access to my project but if you need me to run the calculations using your lat/long values then please post them as text so I can copy and paste them into the project preview.

[cresto.pgaxq2]

Here is a link to the project where the app math is not correct.

https://x.thunkable.com/projects/6587784c856ddf4fb5cabc7d/1bcce8b7-3d25-409a-93b8-75deecebd725/blocks

App says one thing based on Havesine and Google Sheets says another. The google sheets is accurate. App isnt.

[tatiang]

This is what I’ve always used for my Air Quality app and it’s been fine for my needs which are to the nearest 0.25 miles. I haven’t tested it with more specificity than that.

[manyone]

first of all, the formula is approximate (see wiki Haversine formula - Wikipedia) and answer varies depending on where you are on the globe - near the pole or equator - and the proximity of the points you’re measuring.

in your example, if you look at that lat longs for the 2 points,they’re practically adjacent! as if you’re measuring the distance from one corner of your garden to the diagonally opposite corner!

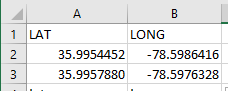
i’ve proved that our thunkable formula works by using this example from Haversine formula - Rosetta Code

and i got an answer of 2887.35km (the average answer is 2887.26+ km).

so i know that the formula works.

however your example hovers on an extreme case - the points are so close

(note: Using 4 decimal places gives a precision of about 11 meters at the equator and about 7 meters at 60 degrees)

after plugging them into into the formula i eventually got these values for variable w and variable v
w=0.345418744
v=0.654581256

if you follow the formula we need to compute acos(w+v) - but w+v happens to be 1.00 and acos(1) function means - how many degrees would an angle be such that its cosine is 1? the answer is , according to trigonometry, supposed to be 0 (zero) - ie. cosine of zero is 1.0

somehow (w+v) is not exactly 1.0 and excel stores the values at a higher precision such that w+v is not exactly 1. hence it is able to return a value for acos(w+v) - a value of 1.54516E-05 (which is a very small value, close to zero)

thunkable’s acos is not so precise - it looks like it’s precise only to 5(6?) decimal points and it comes back with a value of 0.000020 (compared to excel’s 0.0000154516)

so i suggest,you apply this formula only to points that are greater than 1 degree each way - by lat or by long.

the formula works very well for computing distances (approximate) between 2 points that are not adjacent.

[cresto.pgaxq2]

Merry Christmas !!

So better to use KM instead of miles.

Or switch to this formula

[cresto.pgaxq2]

/The Vincenty Formula

[manyone]

You’ll get the same result. The formula we"re using in the thunkable demo i provided (c=acos(sin(lat1(*sin(lar2) … blah blah) is derived from the set of variables you gave. I’ve used all those formula in excel and proved that t single formula so it won’t make a difference.

Merry Christmas to you too!

[cresto.pgaxq2]

I see what you’re saying.

The app I’m creating doesn’t have a static value to calculate on.

Current lat and current long would be live pulls from the device current lat and long.

So if it is really close , the accuracy won’t be there?